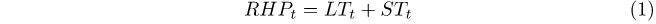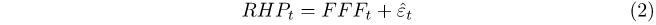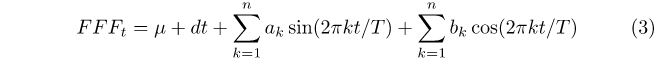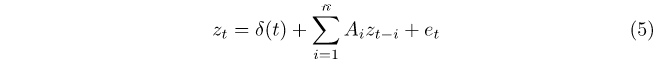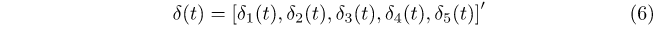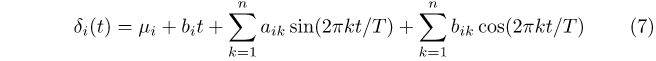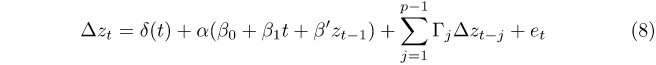- Published by:
- Department of Treasury and Finance
- Date:
- 1 June 2022
Jack McCorkell1,3 and Jonathan Dark2
1 Revenue Forecasting Team, Economic Division, DTF.
2 Department of Finance, University of Melbourne; Revenue Forecasting Team, Economic Division, DTF.
3 For contact author’s details and/or questions on this article, please email: veb@dtf.vic.gov.au
Disclaimer: The views expressed in this paper are those of the authors and do not necessarily reflect the views of DTF.
Suggested Citation: McCorkell J and Dark J (2022) An Application of the Flexible Fourier Form to Australian Housing Market. Victoria’s Economic Bulletin, June,vol 6, no 1. DTF.
Abstract
We apply the Flexible Fourier Form or FFF (a semi-nonparametric non-linear function) to Australian house prices from 1980 to 2021. First, we decompose real house prices into a non-linear long-term (LT) component and a short-term (ST) component. Real house prices and their LT component have a stable long-run relationship (or cointegrate) with income (real disposable income and real GDP), but not when income is on a per capita basis.
This is consistent with real house price growth outpacing growth in income per person, as well as a non-trivial part of overall income growth being caused by population growth. Results also show that the FFF decomposition reveals other cointegrating relations with rent and affordability measures that are undetected when using raw house prices.
Finally, the short‑term component of house prices is shown to be cyclical and strongly related to sales volumes (but not income). Second, we use the FFF to control for structural breaks within Vector Autoregression (VAR) and Vector Error-Correction Models (VECM). Unlike the conventional VAR/VECM, where variables revert to their (constant) unconditional mean, inclusion of the FFF means that each variable reverts to a deterministic value that evolves over time in accordance with smooth structural change. We show that when allowing for structural change, the VAR and VECM yield greater variable interaction and additional insights into the dynamics of Australian house prices.
1. Introduction
The importance of house prices in the Australian and Victorian economies should not be understated.
High and rising house prices generally encourage consumer spending via the wealth effect, increase access to finance by small business owners by increasing available collateral, and bolster state government revenues. At the same time, rising house prices raise concerns about the bursting of house price bubbles and worsening levels of inequality. Recent attempts to change the tax treatment of property through changes to negative gearing and the capital gains tax discount revealed the very difficult trade-offs involved in this important area of public policy. Understanding the relationships between house prices and the macroeconomy is therefore important for all levels of government, the public service, individuals, investors, and the corporate sector.
The literature provides conflicting conclusions regarding the determinants of real house prices over time. One possible explanation is that certain variables affect prices more significantly in the short term, while others may have a stronger relationship with house prices over the long term. In the first part of the paper, we use the Flexible Fourier Form, a periodic (or repeating) semi-nonparametric global approximator of non-linear functions, to decompose real house prices into a smooth long-term trend component and the remaining short-term dynamics. We identify stable long-run (or cointegrating) relationships between the long-term component and income (real disposable income and real GDP). This is not the case when income is on a per capita basis. This is consistent with growth in real house prices outpacing growth in income per person. It is also consistent with a non-trivial part of disposable income and GDP growth being due to population growth. Results also show that the FFF decomposition reveals cointegrating relations with rent and affordability measures that are undetected when using raw house prices. This suggests that the removal of short-term (possibly noisy) variations may help to better identify long-run relationships between macroeconomic variables. In contrast, we show that the short-term component is largely cyclical and strongly related to sales volumes (but not disposable income or real GDP).
An alternative explanation for the lack of consensus regarding house price determinants may be failure to control for structural breaks. Breaks may occur in house prices as well as in their relationship with other macroeconomic variables. Inadequately controlling for breaks may result in significant parameter bias and poor public policy. Even though house prices have largely followed an increasing trajectory over the period examined, they have been exposed to many significant events, including the October 1987 equity market crash, the global financial crisis, and the COVID-19 pandemic. They have also been affected by policy changes over the period, like the significant rise in interest rates in the early 1990s, increases in the capital gains discount in 1999, various federal and state home buyer grant schemes, and declining investment in public housing. These events and policy changes are likely to have caused structural changes to the dynamics of house prices and their relationship to other macroeconomic variables. Some of the described events are sudden and relatively short lived, like October 1987, while others are much slower and more permanent, like the run down in public housing. Either way, housing market frictions like stamp duty and search costs mean that structural change is likely to occur more slowly in the housing market than in financial markets.
In the second part of the paper, we therefore allow for structural change in Australian house prices via the FFF, as it can be used to control for structural breaks and non‑linearities (Enders and Jones 2016; Baillie and Morana 2012). It does not require breakpoint identification procedures and is effective when there are an unknown number of breaks. Further, its flexibility means that it can capture both smooth and slow-moving structural change or much more rapid sharp adjustments (Jones and Enders 2014).1 It therefore seems natural to consider application of the FFF when examining the dynamics of the Australian property market. To our knowledge, this is the first paper to do so.
We apply the FFF as a deterministic regressor within three multivariate models of real house prices, the interbank overnight cash rate, disposable income per capita, housing sales volume, and the unemployment rate. By allowing for time variation in each of the intercept terms via their own FFF, these models allow for smooth structural change and reversion of each variable to its own time varying value. This is in contrast to a standard VAR or VECM, which has a time invariant intercept and reversion of each variable to a constant unconditional mean. We show that controlling for structural change via the FFF results in much richer interaction between variables through Granger-causality tests and Impulse Response Functions. This is consistent with Enders and Jones (2016) who apply a similar approach to US grain and oil prices.
Section 2 of the paper outlines the data employed. Section 3 presents the decomposition of real house prices into long-term and short-term components and explores their relationship with macroeconomic variables. Section 4 specifies three multivariate models with the FFF as an intercept term and explores the implications for Granger-causality testing and impulse response analysis. Section 5 concludes.
Footnotes
[1] This is in contrast to other methods like Bai-Perron (1998) where all breaks are sharp.
2. Data
Research into the determinants of house prices informs the choice of variables for this study.
Identified determinants include income growth (Malpezzi 1990), inflation, GDP, and interest rates (Iacoviello 2002; Aye et al. 2013; Droes et al. 2016; Muellbauer and Murphy 1997), housing sales volume (Zhou 1997), population growth and construction costs (Capozza et al. 2004) and exchange rates (Ya-chen and Shuai 2013).
Table 1 reports summary statistics for the variables employed over the period from 1980Q1 to 2021Q1. Data is collected from the Australian Bureau of Statistics (ABS), the CoreLogic (CL) Economist Pack dataset, the Reserve Bank of Australia (RBA), and the Organisation for Economic Co-operation and Development (OECD). All variables were obtained in seasonally adjusted form, except the cash rate, exchange rate index, and sales volume. We seasonally adjust sales volume via the method employed by the ABS.1
Table 1: Descriptive statistics of the variables employed
| Mean | Std. Dev. | Min. | Median | Max. | Source | |
| Real house price index | 61.87 | 26.96 | 30.21 | 48.93 | 113.90 | OECD |
| Rent price index | 62.25 | 25.87 | 18.81 | 58.14 | 102.52 | OECD |
| Price-income ratio index | 100.00 | 23.11 | 66.41 | 91.84 | 147.57 | OECD |
| Price-rent ratio index | 100.00 | 34.90 | 57.87 | 82.99 | 172.66 | OECD |
| Cash rate | 7.08 | 4.86 | 0.03 | 5.33 | 18.35 | RBA |
| Exchange rate index | 63.88 | 10.49 | 48.73 | 61.67 | 94.13 | RBA |
| Sales volume | 31.44 | 13.09 | 6.33 | 35.44 | 58.50 | CL |
| Real GDP | 287.62 | 117.12 | 134.61 | 261.89 | 516.90 | ABS |
| Disposable income | 234.77 | 90.37 | 119.45 | 215.87 | 422.12 | ABS |
| Real GDP PC | 14.08 | 3.58 | 8.92 | 13.74 | 20.08 | ABS |
| Disposable income PC | 11.56 | 2.67 | 7.76 | 11.31 | 16.41 | ABS |
| Population | 19.64 | 3.21 | 14.68 | 19.13 | 25.74 | ABS |
| Unemployment rate | 6.81 | 1.76 | 4.10 | 6.20 | 11.20 | ABS |
| Employment-population ratio | 59.23 | 2.36 | 54.20 | 59.20 | 62.80 | ABS |
| Participation rate | 63.54 | 1.60 | 60.30 | 63.40 | 66.30 | ABS |
| Consumer price index | 74.13 | 26.30 | 25.40 | 72.90 | 117.90 | ABS |
Note: OECD indices are set to 100 in 2015. The cash rate is the interbank overnight cash rate in percentage. The exchange rate index is the trade weighted exchange rate index, set to 100 in 1970. Sales volume is the quarterly housing sales volume in thousands of units. Real GDP and disposable income are in billions of dollars. Real GDP per capita and disposable income per capita are in thousands of dollars. Disposable income and disposable income per capita are in real, net terms. Population is in millions of people. The unemployment rate, employment-population ratio, and participation rate are in percentages. The consumer price index is set to 100 in 2012. All variables have 165 observations from 1980Q1 to 2021Q1.
Footnotes
[1] This is the X-12 approach with X-11 filter.
3. Macroeconomic decomposition of real house prices
In this section, we decompose real house prices into long-run and short-run components via the FFF.
We then examine the relation between both components and each of the macroeconomic variables.
3.1 Methodology
The FFF can be applied as a smoothing function to extract a long-run non-linear trend. Unlike conventional trend estimators, such as linear or quadratic, the FFF remains agnostic with respect to the trend’s form. This is advantageous, as, for example, a movement that appears to be a shock away from a linear trend may in fact be an underlying non-linear shift.
Li (2021) estimates the risk premium in financial markets by decomposing the observed risk premium into the actual risk premium, which is smooth and time-varying, and a short-term idiosyncratic error. We use a similar specification to define the long‑term and short-term components of real house prices as follows:
where RHPt is the value of the real house price index at time t, and LTt and STt are the long-term and short-term components of the index at time t respectively. We approximate the long-term component of real house prices using a fitted FFF, as follows:
where μ is an intercept term, n is the number of frequencies selected, T is the number of observations, and ak and bk are the coefficients estimated via OLS. The FFF approximates the long-term trend of the series, while the residuals εt from equation (2) approximate short-term fluctuations around the trend.1
The results of the decomposition are shown in Figure 1. Visually, the FFF successfully approximates the non-linear trend, which displays significant growth over the period. In contrast, the short-term component displays cyclical behaviour, with periods above or below the trend generally persisting for two to five years.2
Figure 1: The decomposition of the LT and ST components of RHP in levels
Note: The smoothed function taken as the long-term component is generated by fitting the 3‑frequency Flexible Fourier Form to the RHP series. The ST component is the residual series from the regression, representing fluctuations around the long-term trend.
3.2 Long-term component
We perform Engle-Granger cointegration tests to determine if there are any long-run relationships between house prices and each of the macroeconomic variables. Tests are performed using the raw real house price index and the long-run component extracted via the FFF. We therefore examine whether removal of the short‑run component helps to better identify long‑run relationships between house prices and each of the macroeconomic variables. More specifically, cointegration is present if residuals from the following regression:
are I(0), where Yt is real house prices or its long-run component at time t, and Macrot denotes a macroeconomic variable at time t. Table 2 reports the results from these tests.
Table 2: Results for the pairwise Engle-Granger tests for cointegration
| Raw Levels | LT Levels | |||
| Rent price index | -1.85 | (0.61) | -4.34*** | (0.00) |
| Price-income ratio index | -2.39 | (0.33) | -3.64** | (0.02) |
| Price-rent ratio index | -2.94 | (0.12) | -2.20 | (0.42) |
| Cash rate | -1.22 | (0.85) | -1.28 | (0.84) |
| Exchange rate index | 0.54 | (0.99) | -0.90 | (0.92) |
| Sales volume | -1.19 | (0.86) | -0.93 | (0.92) |
| Real GDP | -3.43** | (0.04) | -2.82 | (0.16) |
| Real GDP PC | -2.40 | (0.33) | -2.38 | (0.34) |
| Disposable income | -3.45** | (0.04) | -4.00** | (0.01) |
| Disposable income PC | -2.54 | (0.26) | -2.60 | (0.24) |
| Population | -2.45 | (0.30) | -2.04 | (0.51) |
| Unemployment rate | -2.24 | (0.40) | -2.45 | (0.30) |
| Employment-population ratio | -2.38 | (0.33) | -2.50 | (0.28) |
| Participation rate | -2.13 | (0.46) | -2.24 | (0.40) |
| Consumer price index | -2.46 | (0.30) | -2.57 | (0.25) |
Note: the first and third columns show the T-statistics from the tests, and the numbers in parentheses are the corresponding p-values. Significance: 10%*, 5%**, 1%***.
Table 2 reveals that both the raw series and the long-term component of real house prices cointegrate with real disposable income. However, our results indicate that neither series cointegrate with real disposable income per capita. This suggests that although there may be a stable long-term relationship between house prices and disposable income, this does not hold when income is measured in per capita terms. A similar observation can be made for real GDP and real GDP per capita in the results for the raw series – prices share a stable relationship with overall real GDP, but not real GDP per capita.3 This suggests that real house price growth has outpaced income growth per person, and that a significant part of the growth in disposable income and GDP has occurred because of population growth. This has fuelled income growth overall, keeping the relation between income and real house prices stable.
An interesting finding is the detection of cointegration between real house prices and the rent price index once the FFF has been applied to remove fluctuations. This suggests that over the long-term, rents and prices tend to move together. Similarly, the FFF decomposition reveals a relationship between the long-term component of prices and the price-income ratio, an affordability measure capturing the ratio of nominal house prices to nominal disposable income per person. This is consistent with our finding of no cointegration with the per capita GDP or disposable income above. This points to houses having become less affordable as house price growth has outpaced per capita income growth.
Finally, it is worth mentioning that there is no long-run relation between house prices and sales volume. However, we will see that volumes have a strong relation with the short-term component of house prices.
In summary, the long-term component of RHP has a stable long-run relation with macroeconomic aggregates like disposable income and GDP, as well as rent and affordability, but these relations may be unidentified in the presence of short-term (possibly noisy) fluctuations in house prices. The long-run relation between RHP and income (i.e. disposable income or real GDP) does not hold when either income measure is on a per capita basis. This is due to a non-trivial part of the growth in income being due to population growth.
3.3 Short-term component
Figure 1 reveals that the short-term component displays cyclical behaviour around the nonlinear trend, with deviations above or below the trend lasting around two to five years. Because the short-term component is I(0), we use an Autoregressive Distributed Lag (ARDL) model. This enables us to explore any correlation or predictive relationships with other variables, using a mix of I(0) and I(1) variables.4 We set the number of lags on the dependent variable to one and use the SIC to determine the number of lags for each regressor, up to a maximum of four.
Table 3: The estimation results from seven ARDL regressions
| Dependent variable: Short term component of real house price index (levels) | |||||||
| Variable | (1) | (2) | (3) | (4) | (5) | (6) | (7) |
| SR component of RHP(-1) | 0.908*** | 0.893*** | 1.045*** | 1.030*** | 0.911*** | 1.023*** | 1.049*** |
| Cash rate | -0.026 | -0.011 | 0.019 | 0.047 | 0.151 | 0.024 | |
| Cash rate (-1) | -0.232** | ||||||
| Exchange rate | 0.112*** | 0.023*** | 0.032*** | ||||
| Exchange rate (-1) | 0.000 | ||||||
| Exchange rate (-2) | -0.110*** | ||||||
| Disposable income PC | 0.158 | -0.089 | |||||
| Disposable income PC (-1) | -0.132 | ||||||
| Disposable income PC (-2) | -0.449 | ||||||
| Disposable income PC (-3) | -2.216*** | ||||||
| Disposable income PC (-4) | 2.523*** | ||||||
| Sales volume | 0.051* | 0.063** | 0.065** | 0.049* | |||
| Sales volume (-1) | 0.145*** | 0.145*** | 0.145*** | 0.145*** | |||
| Sales volume (-2) | -0.004 | -0.003 | -0.005 | -0.005 | |||
| Sales volume (-3) | -0.059 | -0.059 | -0.060 | -0.059 | |||
| Sales volume (-4) | -0.112*** | -0.108*** | -0.098*** | -0.113*** | |||
| Constant | 0.234 | 0.046 | -0.897 | -3.120*** | 2.053** | -2.717** | -0.568* |
| R-squared | 0.802 | 0.825 | 0.887 | 0.892 | 0.834 | 0.899 | 0.886 |
| Adjusted R-squared | 0.800 | 0.820 | 0.882 | 0.886 | 0.825 | 0.892 | 0.882 |
| SIC | 3.387 | 3.357 | 2.999 | 2.986 | 3.415 | 3.003 | 2.970 |
| AIC | 3.330 | 3.243 | 2.846 | 2.814 | 3.242 | 2.811 | 2.836 |
The variables used are as follows. Cash rate: the interbank overnight cash rate in percent. Exchange rate: the trade weighted exchange rate index for the Australian dollar. Disposable income PC: the real net disposable income per capita in Australia, in 1000s of AUD. Sales volume: housing sales volume per quarter, in 1000s of units. Models are selected with SIC. All variables are integrated of order 0 or 1 according to the Augmented Dickey-Fuller test. Significance: 10%*, 5%**, 1%***.
Table 3 presents results from seven ARDL specifications. In all regressions, the autoregressive coefficient is significant at 1 per cent and highly persistent. This is consistent with sustained periods above or below the long-run trend. The most notable result from these regressions is the highly significant coefficients on both the contemporaneous and lagged values of sales volume in regressions (3), (4), (6), and (7). These coefficients remain significant even when the cash rate, the exchange rate, and disposable income are included as additional regressors, indicating that sales volume may be highly predictive of short-term fluctuations in real house prices. There may be some cyclical behaviour being captured by the positive coefficients for the contemporaneous and first lag values, and by negative coefficients for longer lags.
The cash rate is not significant contemporaneously in any of the regressions. However, its first lag is negatively correlated with the short-term component at the 5 per cent level in regression (5). The predictive relationship of the cash rate on short‑term fluctuations may come through its influence on exchange rates, which is significant at the 1 per cent level in regressions (2), (4), and (6). Disposable income per capita does not have a contemporaneous relationship with the short-term component, but regression (5) shows that it may be predictive at three or four lags. However, this relationship disappears when sales volume and the exchange rate are accounted for in regression (6).
Of the six regressions, regression (7) minimises the SIC, and has the third-lowest AIC, suggesting that it is the best explanatory model for the short-term component of real house prices. This model only includes sales volume, indicating that it may be one of the most important predictors of short-term fluctuations in the Australian housing market. Regression (4) also features a low SIC and AIC, suggesting that perhaps the cash rate and trade-weighted exchange rates are helpful at predicting short-term fluctuations.
In summary, the decomposition of house prices into long-term and short-term components enables us to uncover additional macroeconomic linkages with house prices. Cointegration or long-term relationships are seen between real house prices and income (disposable income and real GDP), rents, and the price-to-income ratio. When income is on a per capita basis, there is no longer a stable long-run relation with house prices. The ARDL models suggest that sales volume has a strong contemporaneous and lagged relationship with house prices in the short-term, which is consistent with Zhou (1997).
Footnotes
[1] We limit the number of trigonometric frequencies (n) in equation (3) to a maximum of three. This means that a smoother fit is generated, thereby better approximating the overall trend without capturing short‑term fluctuations. Three frequencies are ultimately selected, as this minimises the Schwarz Information Criterion (SIC) for the regression on equation (3), compared to one or two frequencies.
[2] We also extract the long-term and short-term components of real house prices in logs as this helps remove some of the nonlinearities by reducing the impact of large fluctuations. The results are similar.
[3] Prices are no longer cointegrated with real GDP once the FFF has been applied, but due to the lack of power of the ADF test, there may still be a relationship with real GDP (p-value of 0.16), but there is unlikely to be one with real GDP per capita (p-value of 0.34).
[4] We are careful not to make any causal interpretation, as this requires weakly exogenous independent variables. Significant coefficients can also be the result of spurious regression if the ARDL bounds test indicates no cointegration. Interpretation must be mindful of omitted variables and other sources of endogeneity that may bias the results.
4. Controlling for structural breaks in a VAR
Structural breaks, or parameter instability, can refer to changes in the dynamics of a single time series or to changes in the relationships between series.
The literature generally points to the importance of both forms of structural break when modelling house prices. Droes et al. (2016) find a shift over time in the importance of different variables (population growth, new housing supply, income, interest rates) on the housing market in Amsterdam. Aye et al. (2013) identify structural breaks in the South African housing market and control for these via Structural Vector Autoregression (SVAR). A strengthening of the relationship between US house prices and macroeconomic variables (private consumption and economic activity) is found by Ahamada and Diaz Sanchez (2013). Muellbauer and Murphy (1997) model structural breaks in the bivariate relation between house prices and income and house prices and interest rates.
The most common ways to account for structural breaks are breakpoint regression, threshold regression and Markov switching. All of these approaches tend to be heavily parameterised, as each additional regime requires estimation of a new set of parameters. To maintain tractability, very often the number of regimes is small. Markov switching models, for example, very often limit the number of regimes to two, otherwise estimation issues, such as failure to converge or sensitivity of estimates to starting values, often arise. Breakpoint and threshold regression also require breakpoint identification, and threshold regression requires a suitable threshold variable. An alternative to these models is to use a dummy variable approach. Enders and Jones (2016) identify that these approaches can be effective when there are a small number of sharp breaks or additive outliers but will not be as capable of detecting mean shifts if the breaks are sufficiently smooth (innovative outliers).
The FFF overcomes all of these limitations. Allowing for structural change via the FFF does not require breakpoint, regime, or dummy identification, and when incorporated into a VAR, the model can still be easily estimated via OLS. To our knowledge, we are the first paper to control for structural breaks in the Australian housing market in this way.
The use of the FFF to control for structural breaks is a recent development, so academic studies are limited. Enders and Jones (2016) incorporate the FFF into a VAR between oil and grain prices. They note that structural breaks within a VAR are generally more complicated to deal with than in a univariate setting due to the interrelationships between variables. It can be difficult to determine if a break in one of the variables is due to a break in its own series, or whether it is a break that is being transmitted from one of the other series.
The results of Enders and Jones (2016) confirm Ng and Vogelsang’s (2002) finding that Granger-causality tests are mis-sized when structural breaks are unaccounted for. As a result, they find that Granger-causality tests identify much richer relationships between variables when employing the FFF. They also show additive and innovative outliers can be controlled for by the FFF, and that it can effectively capture sharp and smooth breaks. This contrasts with Bai and Perron’s (1998) methodology, which performs poorly in the presence of smooth breaks. Given the housing market frictions discussed earlier, structural breaks are likely to be smooth, so the FFF seems a prudent way to proceed.
4.1 Methodology
In this section, we examine the impact of controlling for structural breaks via the FFF when modelling Australian house prices. For robustness and comparative purposes, we consider a VAR in levels with a time trend, a VECM, and a VAR in first-differences.1 We compare the standard version of each model, which does not control for breaks, with the FFF version of the model, which does control for breaks. To examine model differences, we focus on Granger-causality tests, as they are mis-sized in the presence of breaks.2 All models select the optimal lag via the Schwarz Information Criterion. Our choice of variables is based on our analysis in Section 3 and contemporary literature.
The FFF-VAR is specified as:
where zt is a (5 × 1) vector (RHP, cash rate (%), disposable income per capita ($000’s), sales volume (000’s), unemployment rate (%)), Ai is a (5 × 5) coefficient matrix for lag i, et is a (5 × 1) vector of error terms and all variables are in levels. The δ(t) term in equation (5) is defined as:
with each time-varying intercept δi(t) depending on n Fourier frequencies in the following way:
where μi is a constant, bit is a linear time trend, T is the total number of observations in the sample, and aik and bik are coefficients on the trigonometric terms. We use the SIC to jointly select the lag length and the order of the FFF for our models. For this VAR, a lag length of 1 and a trigonometric order of n = 3 is selected. Conventional VARs without the FFF are nested within the FFF-VAR. A non-FFF VAR with a linear time trend imposes aik=bik=0 for all i and k, and a VAR in first-differences additionally imposes bit = 0.
The FFF-VECM is specified as:
with the same definitions as the FFF-VAR above. Γj is a (5 × 5) coefficient matrix for lag j. The time varying intercepts within δ(t) do not include a time trend, that is, bit = is imposed. As above, the conventional VECM is specified in the same way, but with the additional restrictions of aik = bik = 0. This specification (restricted intercept and restricted trend in the cointegrating vector) is selected as it should be used in the presence of deterministic and stochastic trends (Johansen 1995). RHP, the cash rate and the unemployment rate are likely to have stochastic trends, but sales volume is much more likely to grow deterministically over the long run with population.
4.2 Results
Table 4 presents Granger-causality tests for the six models. Parameter estimates and other details for all models are available on request. Panels A, C, and E show the models without the FFF, whereas panels B, D, and F show the FFF-augmented versions of each model. Sales volume clearly Granger-causes (GCs) house prices in all VARs. Real house prices also GC sales volume in all models, but not to the same degree. The cash rate and unemployment rate both GC each other in every model. The unemployment rate GCs real house prices at the 1 per cent level in two of the FFF models (panels B and F), but that relationship is not detected in the other models.
Comparing panels A and B, it is clear that the FFF-VAR can detect Granger- causal relationships that the linear VAR is unable to capture. For instance, only sales volume Granger-causes RHP in panel A, but both disposable income per capita and the unemployment rate Granger-cause RHP at the 5 per cent level or better in panel B. A similar result is seen in panels E and F, with the FFF-VECM detecting relationships that the regular VECM fails to find. Panels C and D are very similar in their detection of Granger-causal relationships, indicating that the FFF is not as important when the data is differenced. These results are consistent with the findings of Enders and Jones (2016), who show that unaccounted structural breaks can cause Granger-causality tests to be mis-sized. Panels B and F detect more economically sound relationships than panels A and E respectively, as they control for structural breaks using the FFF. The same effects are clearly not present in the first-difference models. This is consistent with structural breaks in long‑term dynamics that are removed by differencing.
We now compare the impulse response functions for real house prices in Figure 2. In the interest of brevity, we only present three models: the FFF-VECM, the FFF-VAR with linear trend, and the regular VAR in first-differences.3
Table 4: Granger-causality results from the six models examined
| RHP | CR | DI PC | SV | UR | |
| A: VAR in levels with time trend | |||||
| Real house prices | – | 6.54** | 2.27 | 16.18*** | 3.94 |
| Cash rate | 1.35 | – | 3.18 | 1.91 | 12.41*** |
| Disp. inc. PC | 0.28 | 1.17 | – | 5.14* | 2.09 |
| Sales volume | 59.75*** | 2.64 | 2.32 | – | 3.64 |
| Unemployment rate | 2.00 | 11.53*** | 3.34 | 7.01** | – |
| B: FFF-VAR in levels with time trend | |||||
| Real house prices | – | 10.76*** | 2.19 | 19.49*** | 8.44*** |
| Cash rate | 0.54 | – | 4.12** | 0.08 | 9.80*** |
| Disp. inc. PC | 6.41** | 0.97 | – | 0.04 | 0.66 |
| Sales volume | 163.02*** | 0.54 | 0.25 | – | 4.73** |
| Unemployment rate | 12.87*** | 33.52*** | 5.41** | 1.71 | – |
| C: VAR in first-differences | |||||
| Real house prices | – | 4.59** | 0.04 | 6.36** | 5.77** |
| Cash rate | 0.51 | – | 0.55 | 1.64 | 5.23** |
| Disp. inc. PC | 0.32 | 0.67 | – | 3.05* | 2.07 |
| Sales volume | 66.33*** | 0.58 | 1.44 | – | 4.35** |
| Unemployment rate | 1.16 | 8.24*** | 1.39 | 5.09** | – |
| D: FFF-VAR in first-differences | |||||
| Real house prices | – | 4.72** | 0.00 | 5.47** | 5.28** |
| Cash rate | 0.55 | – | 0.63 | 1.65 | 5.62** |
| Disp. inc. PC | 0.21 | 0.59 | – | 3.14* | 1.92 |
| Sales volume | 68.73*** | 0.61 | 1.55 | – | 4.29** |
| Unemployment rate | 1.08 | 8.55*** | 1.23 | 5.00** | – |
| E: VECM in levels | |||||
| Real house prices | – | 9.30*** | 0.06 | 0.34 | 6.50** |
| Cash rate | 0.59 | – | 0.57 | 0.42 | 5.81** |
| Disp. inc. PC | 0.35 | 0.37 | – | 4.66** | 2.30 |
| Sales volume | 65.92*** | 0.28 | 1.46 | – | 4.69** |
| Unemployment rate | 1.25 | 6.35** | 1.29 | 8.34*** | – |
| F: FFF-VECM in levels | |||||
| Real house prices | – | 2.25 | 7.15** | 15.96*** | 2.72 |
| Cash rate | 4.99* | – | 5.60* | 0.02 | 6.79** |
| Disp. inc. PC | 6.05** | 0.01 | – | 4.84* | 9.30*** |
| Sales volume | 37.04*** | 5.20* | 2.88 | – | 4.40 |
| Unemployment rate | 9.37*** | 7.23** | 7.04** | 5.57* | – |
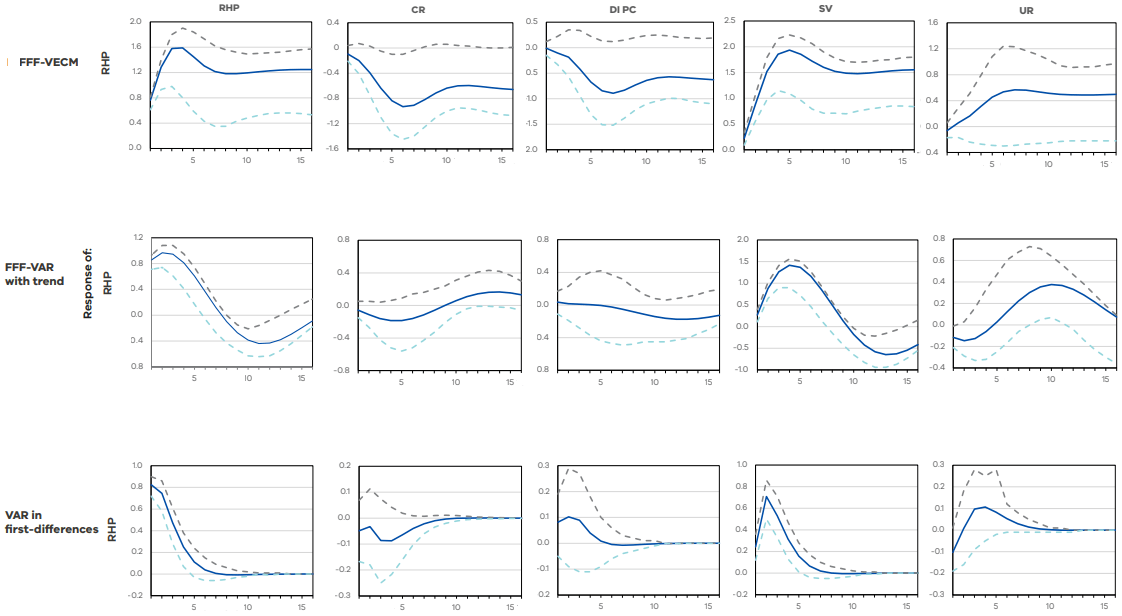
Figure 2: The generalised impulse responses of real house prices
Response to generalised one S.D. innovations
95% CI using standard percentile bootstrap with 1000 bootstrap reps
Shock to:
Note: shown are the generalised impulse responses of real house prices to a one standard deviation shock for each of the variables in the system. The FFF-VECM is in row 1, the FFF-VAR with linear trend is in row 2, and the VAR in first-differences is in row 3. The solid line shows the impulse response, and the dashed lines show the 95 per cent confidence interval using the standard percentile bootstrap with 1000 replications. Variables are as follows. RHP: Real house price index, CR: Interbank overnight cash rate, in per cent, DI PC: disposable income per capita in thousands of AUD, SV: housing sales volume in thousands of units, UR: unemployment rate in per cent. The shock is at period 0, and 16 periods are shown in each graph.
There is a notable difference in the size and persistence of the impulse responses from the FFF-VAR and FFF-VECM compared to the linear VAR in first‑differences. This is to be expected, as differencing removes the long-run dynamics.4 We also note that the higher levels of persistence to shocks in the VECM is due to the cointegrating relation between variables that is not present in the VAR in levels.
The FFF-VECM suggests that a positive shock to real house prices will be persistent over the following four years, but the FFF-VAR IRF implies that a correction may occur after approximately 10 quarters. Both the FFF-VAR and FFF-VECM IRFs show that a positive shock to the cash rate does not have a statistically significant effect on real house prices, although the FFF-VECM suggests a small downward movement could occur. Disposable income per capita does not have a statistically significant effect on prices in all three models. Sales volume has a large impact on house prices, with all three models indicating that prices will increase for at least a year after a positive volume shock. This is consistent with the ARDL findings in Section 3.3. The FFF‑VECM suggests this effect will be persistent for at least four years, while the FFF‑VAR suggests a slight correction after two years. Finally, a shock to the unemployment rate does not have a significant effect on prices in any of the models, although there is some indication in the FFF-VAR model that this shock could cause a delayed increase in prices after two years. This is likely due to the easing of monetary policy in response to a weakening economy and labour market.
Footnotes
[1] We also test a VAR in levels without a time trend, but this model has been discarded due to roots within the unit circle.
[2] We also examine the Granger-causality results for the VECM in logs and VAR in log first-differences, reported in the appendix. The linear VAR in logs has inverse roots outside of the unit circle even with the inclusion of a time trend, so it is not reported.
[3] The regular VAR and VECM show similar IRFs to their FFF counterparts, but the size and significance of the impulses is reduced, consistent with these models’ inability to fully capture variable interrelationships when structural breaks are present.
[4] While first-differencing can mitigate some of the issues caused by the presence of structural breaks, namely mis-sized Granger-causality tests, we are certainly not advocating the abandonment of the VAR or VECM in levels given the importance of long-run dynamics in the economy.
5. Conclusion
We apply the FFF to Australian house prices from 1980 to 2021.
The FFF is initially used to decompose house prices into a nonlinear long-term component and a transitory or short-run component. We use this decomposition to examine the relation between house prices and macroeconomic variables across the different time scales. We identify long-run relationships between house prices and income (real disposable income and real GDP). This was not so when both income measures were on a per capita basis. This is consistent with growth in real house prices outpacing growth in income per person. It is also consistent with a non-trivial part of disposable income and GDP growth being due to population growth.
It is worth highlighting that cointegration does not necessarily imply causation. However, our results do indicate that house prices and income (disposable or GDP) move together over the long run. There are economic forces at play that ensure that if house prices and income deviate from their long run relationship, a process of adjustment will occur to restore the long-run equilibrium. This relation, however, does not hold when considering income on a per capita basis. This raises obvious concerns regarding intergenerational wealth inequality and the difficult policy trade-offs involved.
Our results also show that the FFF decomposition reveals cointegrating relations with rent and affordability measures that are undetected when using raw house prices. Removal of short-term (possibly noisy) dynamics may therefore help to better identify long-run relationships between macroeconomic variables. Finally, we show that the short-term component of house prices displays cyclical behaviour that is strongly related to sales volumes but not income (disposable income or real GDP).
We then use the FFF to control for structural breaks in a VAR and VECM between real house prices, the cash rate, real disposable income per capita, housing sales volume, and the unemployment rate. We find that structural breaks are more important for the long-run dynamics (via a VAR in levels or VECM), than the short-run dynamics (via a VAR in first-differences). We also show that allowing for structural breaks can help better identify Granger-causality. Our models with structural breaks identified sales volumes, disposable income per capita and the unemployment rate as influential variables, with cash rates playing a lesser role. In contrast, models that failed to allow for breaks only identified sales as important. Failure to allow for structural breaks can therefore misrepresent important interrelationships between macroeconomic variables. This failure may result in poor decision making and policy outcomes.
Further research will examine the out-of-sample forecast performance of the approach. Given the FFF-VAR and FFF-VECM allow forecasts to revert to a time varying value (that evolves according to structural change), this should improve forecast performance relative to a standard VAR (where forecasts revert to the unconditional mean). Improvements may not be significant over short-term horizons but are more likely to be important for medium to long-term forecasts.
6. References
References for this Victoria’s Economic Bulletin research article.
Ahamada I and Diaz Sanchez JL (2013) ‘A retrospective analysis of the house prices macro-relationship in the United States’, World Bank Policy Research Working Paper, 33(6549).
Aye G, Gupta R, Kaninda A, Nyakabawo W and Razak A (2013) ‘House price, stock price and consumption in South Africa: A structural VAR approach’, Corporate Ownership and Control, 10:583–590.
Bai J and Perron P (1998) ‘Estimating and testing linear models with multiple structural changes’, Econometrica, 66(1):47–78.
Baillie RT and Morana C (2012) ‘Adaptive ARFIMA models with applications to inflation’, Economic Modelling, 29(6):2451–2459.
Capozza DR, Hendershott PH and Mack C (2004) ‘An anatomy of price dynamics in illiquid markets: Analysis and evidence from local housing markets’, Real Estate Economics, 32(1):1–32.
Droes M, van de Minne A. (2016) Do the determinants of house prices change over time? Evidence from 200 years of transactions data, technical report, European Real Estate Society (ERES).
Enders W and Jones P (2016) ‘Grain prices, oil prices, and multiple smooth breaks in a VAR’, Studies in Nonlinear Dynamics & Econometrics, 20(4):399–419.
Iacoviello M (2002) ‘House prices and business cycles in Europe: A VAR analysis’, Boston College Working Papers in Economics, 540(1):81-124.
Johansen S (1995) Likelihood-based inference in cointegrated vector autoregressive models, Oxford University Press, Oxford.
Jones PM and Enders W (2014) ‘On the use of the Flexible Fourier Form in unit root tests, endogenous breaks, and parameter instability’, in Ma J and Wohar M (eds) Recent Advances in Estimating Nonlinear Models, Springer.
Li J (2021) ‘On estimating risk premium with Flexible Fourier Form’, Economics Bulletin, 41(3):1026–1035.
Malpezzi S (1990) ‘Urban housing and financial markets: some international comparisons’, Urban Studies, 27(6):971–1022.
Muellbauer J and Murphy A (1997) ‘Booms and busts in the UK housing market’, The Economic Journal, 107(445):1701–1727.
Ng S and Vogelsang T (2002) ‘Forecasting autoregressive time series in the presence of deterministic components’, The Econometrics Journal, 5(1):196–224.
Ya-chen L and Shuai Z (2013) ‘Econometric analysis on the relationship between RMB exchange rate and real estate price by VAR model’, 2nd International Conference on Science and Social Research, 428–430.
Zhou Z (1997) ‘Forecasting sales and price for existing single-family homes: a VAR model with error correction’, Journal of Real Estate Research, 14(2):155–167.
7. Appendix
Table 5: Granger Causality results from the three log models examined.
| RHP | CR | DI PC | SV | UR | |
| A: FFF-VECM in logs | |||||
| Real house prices | - | 2.08 | 0.09 | 5.35** | 5.53** |
| Cash rate | 2.05 | - | 7.37*** | 1.26 | 0.95 |
| Disp. inc. PC | 2.79* | 3.83* | - | 0.19 | 5.34** |
| Sales volume | 17.39*** | 5.19** | 0.53 | - | 0.66 |
| Unemployment rate | 2.93* | 0.68 | 10.33*** | 2.97* | - |
| B: VAR in log first-differences | |||||
| Real house prices | - | 2.98* | 0.13 | 5.17** | 12.77*** |
| Cash rate | 0.11 | - | 11.02*** | 4.81** | 1.26 |
| Disp. inc. PC | 0.72 | 9.05*** | - | 3.16* | 6.15** |
| Sales volume | 37.64*** | 0.06 | 0.67 | - | 1.03 |
| Unemployment rate | 1.49 | 1.13 | 10.39*** | 4.90** | - |
| C: FFF-VAR in log first-differences | |||||
| Real house prices | - | 1.66 | 0.12 | 6.59** | 10.59*** |
| Cash rate | 0.05 | - | 10.74*** | 7.10*** | 1.18 |
| Disp. inc. PC | 0.79 | 8.44*** | - | 4.04** | 5.62** |
| Sales volume | 38.31*** | 0.34 | 0.63 | - | 0.97 |
| Unemployment rate | 1.84 | 1.40 | 10.48 | 4.72** | - |
Note: The VECM in logs did not have all inverse roots within the unit circle, so it is not reported here. Each element is the F-statistic that the row variable Granger-causes the column variable. The following abbreviations apply. RHP: Real House Price index, CR: Cash rate, DI PC: Disposable income per capita, SV: Sales volume, UR: Unemployment rate. Significance: 10%*, 5%**, 1%***.