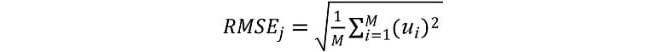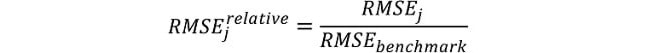4. The forecasting exercise

4.1 Design of the study

This forecasting exercise is performed in pseudo real time, which means that we never use information that is not available at the time the forecast is made but do use final vintage data. We use quarterly taxation revenue from DTF. Our baseline analysis spans from June 1992 to December 2019, which amounts 111 quarterly observations. Our target variables are the growth rates (log-difference) of payroll tax and land transfer duty revenue. In our baseline results, we use a total of 23 economic variables. These variables include property market price and sales indices provided by CoreLogic as well as macroeconomic and labour market statistics provided by the ABS. In later tests, we increase the number of features to 166 in order to assess the performance of machine learning algorithms within a data-rich environment.

This study uses a fixed estimation window method. Except for the random walk model, we employ four-quarter lagged information in other algorithms to conduct forecasting. We train our models using the first 71 observations and test the out-of-sample forecast performance in the last 40 observations (equivalent to 10 years). The hyperparameters of our machine learning methods are tuned using the K-fold cross validation method. The basic idea behind K-fold cross validation is to split the available data into K subsets of folds, then the model is trained and tested K times, with a different fold held out as the validation set each time. The biggest advantage of using K-fold cross‑validation is that it provides a more accurate estimate of the model’s performance than a single validation set, especially when the data size is small. Following common practices, we set K to be 5.

4.2 Forecast evaluation

Evaluations of predictive accuracy are conducted on the basis of computed errors for forecast horizons h = 1, 2, 3, 4 for algorithm j = 1, 2,…, 9. We perform forecast evaluations on the basis of two measures: (i) relative root mean squared errors (RMSE) and (ii) the Diebold and Mariano (DM) test.¹

The root mean squared errors are computed for each algorithm and horizon as follows:

where ui is the forecast error of the algorithm in the testing period. M is the total number of observations in the out-of-sample testing period. The relative RMSEs are then obtained as ratios of each algorithm’s RMSE to the RMSE of the benchmark model:

Footnotes

^{[1] DM test was proposed by Diebold and Mariano (1995) to statistically compare the predictive accuracy of two competing forecasting models. The basic idea is to test whether the forecast errors of the competing forecasting models is statistically different. The null hypothesis of the test is that the two models have the same forecasting accuracy, while the alternative hypothesis is that the forecast errors of one is significantly smaller than the other, implying superior performance.}