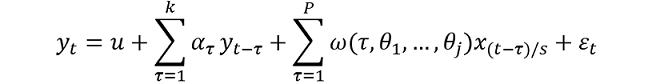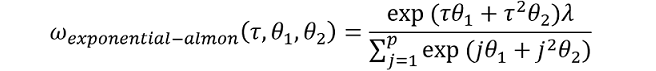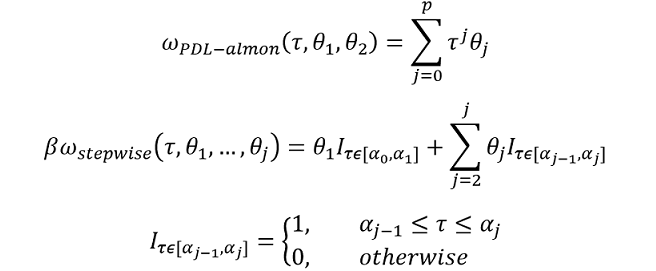2. The MIDAS class of models

Datasets containing variables at different frequencies therefore typically convert all variables to the lowest common frequency. An alternative solution offered by the MIDAS framework is to use a weight function to hyper-parameterise lag coefficients. In its general form, the univariate AR(k)-MIDAS model can be specified as:

where y_t is the low-frequency dependent variable with k lags; x_t is the high-frequency variable at lag (t − τ)/s with p lags; s denotes the number of high-frequency observations for each low-frequency observation and ω(τ,θ₁,…,θ_j) is the hyper-parameterised weight function.

A number of weight functions exist including the Exponential-Almon, Beta, PDL‑Almon and Stepwise functions. The Exponential-Almon specification provides a flexible and parsimonious function and is the workhorse of the literature:

Weights decrease at different rates as the number of lags increase, which allows the data to determine the optimal lag length. While this avoids a priori parameter choices, the models are estimated numerically and may experience convergence problems and unstable coefficients.

The PDL-Almon and Stepwise specifications are estimated analytically and are therefore better suited to experiments using rolling or expanding windows. Both models however require a priori parameter choices and are defined as (Ghysels 2016):

The PDL-Almon requires an a priori polynomial order and lag length choice, with incorrect values risking biased and inconsistent estimates (Hendry et al. 1984). Similarly, the Stepwise function requires a choice of step-size.

The MIDAS framework has been extended in many ways including; unrestricted MIDAS, asymmetric MIDAS, and Markov-switching MIDAS (see Foroni and Marcellino 2013 for a review). Other extensions vary the form and number of regressors, including Autoregressive Distributed Lag (ARDL) MIDAS and MIDAS specifications with more than one high‑frequency predictor. This latter model is less common given parameter proliferation, so model combinations or latent factors are typically employed.