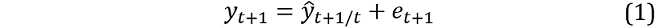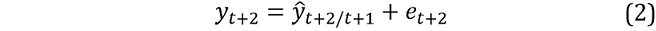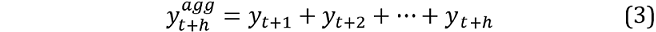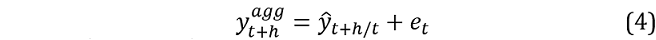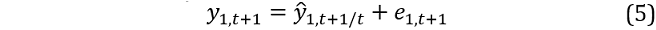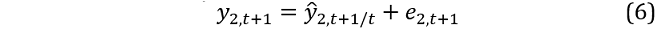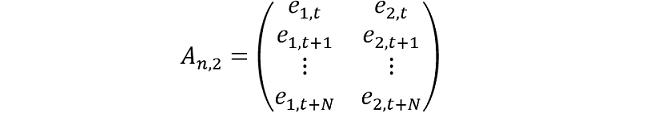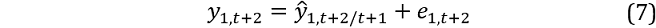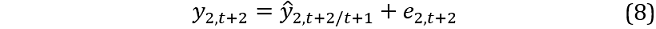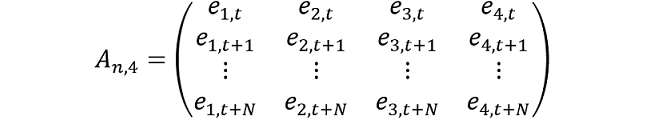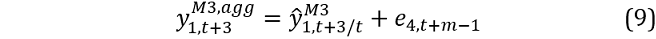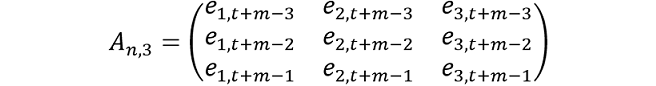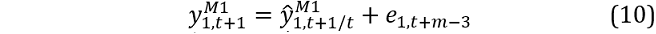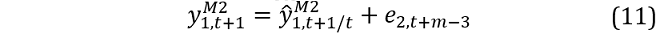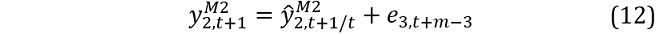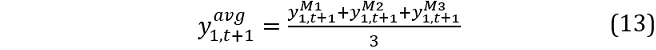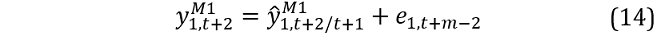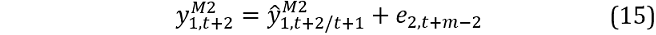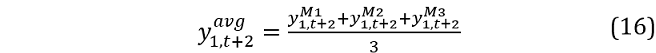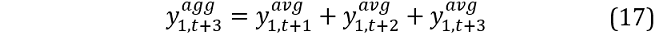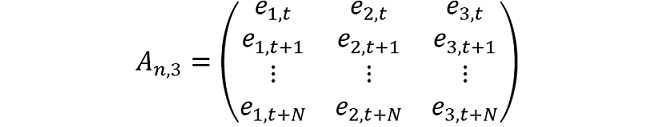3. Bootstrapped prediction interval estimation

We start with univariate models that forecast iteratively. We then consider direct forecasts and generalise to a system of equations. Section 3.2 then develops our proposed methodology for prediction interval estimation when combining direct and iterated forecasts.

3.1 Prediction intervals for individual models

We commence with the construction of h‑step ahead prediction intervals for models that generate forecasts iteratively. Let ŷ_t+1 denote the one‑step ahead forecast from a model for time t + 1 conditional on the information set at time t. The bootstrapped series at time t + 1 is obtained via:

where e_t+1 is a bootstrapped residual. Conditional on the simulated y_t+1 from equation 1, the next period’s one‑step ahead forecast conditional on t + 1 is generated (ŷ_t+2/t+1) and the bootstrapped series at time t + 2 is:

where e_t+2 is the second period’s bootstrapped residual. This process continues until the desired horizon (h) and the value of y_t over horizon h obtained via aggregation:

This process is repeated a large number of times, and the relevant percentiles of the simulated distribution for used to construct the Pls.

For models that use direct forecasts (e.g. MIDAS), only one bootstrapped residual is required. This is because the dependent variable in a model that employs direct forecasts is the aggregated value of y_t over horizon h.

The similated value over horizon is therefore obtained via:

where ŷ_t+h/t is the direct forecast conditional on time t and e_t is a bootstrapped residual.

The bootstrapped procedure for models that employ iterated forecasts is easily extended to a system of equations. We will illustrate using a two variable VAR(1), but this can be easily generalised to models with a higher number of variables and lags. Let ŷ_1,t+1/t (ŷ_2,t+1/t) denote the one‑step ahead forecast of the 1st (2nd) variable at time t + 1 conditional on the information set at time t. The first variable (y_1,t) is our variable of interest. We jointly simulate both series at time t + 1 via:

where e_1,t+1 and e_2,t+1 denote a random draw of the residuals at a point in time. To illustrate, consider a VAR estimated using N observations. The N × 2 matrix of residuals is:

To preserve the correlation across series, a random draw of a row (e.g. row m) is input into equations 5 and 6 i.e. e_1,t+m-1=e_1,t+1 and e_2,t+m-1=e_2,t+1.

Conditional on the simulatedy_1,t+1 and y_2,t+1 from equations 5 and 6, we generate a revised set of one‑step ahead forecasts conditional on t + 1 (ŷ_1,t+2/t+1,ŷ_2,t+2/t+1) and add another randomly drawn row of bootstrapped residuals:

This continues until horizon h and obtained via aggregation (equation 3).

3.2 Prediction intervals for model averages of iterated and direct forecasts

We now modify the above approach to construct PIs around a forecast that is based on a combination of iterated and direct forecasts. Prediction intervals for a model average based on iterated or direct forecasts are a special case of what follows. We briefly outline both special cases at the end of this section.

We need to preserve the dependence structure across models in the forecast combination. For each replication we also seek to generate a single simulated series (y_1,t+1,…,y_1,t+h) that represents the average across all models at each point in time. We therefore ensure that iterated forecasts from t + 1 to t + h, contain the information in all model forecasts.

To illustrate, we consider a three‑step ahead model average forecast (h = 3) consisting of three models: AR(1), bivariate VAR(1), and MIDAS. The AR(1) and VAR(1) models are fit to N monthly observations. The MIDAS model regresses a dependent variable constructed as the sum of the monthly dependant variable over the next quarter (y_1,t+1+y_1,t+2+y_1,t+3) against a high frequency regressor at time t. We assume the MIDAS model is estimated at the same frequency as the AR(1) and VAR(1) i.e. each month. This means the dependent variable in the MIDAS regression is overlapping, and the residual vectors from all models (AR(1), VAR(1) and MIDAS) have the same length N. We construct the N × 4 matrix of residuals as:

where e_1,t denotes the residuals at time t from the AR(1) model (first column), e_2,t and e_3,t the residuals from the bivariate VAR(1) (second and third column), and e_4,t the residuals from the MIDAS model (fourth column). Further, let denote the monthly simulated value of the dependant variable y_1,t at time t, for the AR(1), VAR(1) and MIDAS models respectively.

The AR and VAR models generate forecasts of the dependent variable each month, but the MIDAS model only generates an aggregated forecast for the quarter. To generate a simulated average (that is a function of the three models) for each month, we linearly allocate the bootstrapped MIDAS series over months one, two and three. We commence by randomly drawing a row of residuals, say row m from A_n,4. On adding e_4,t+m-1 to the forecast from the MIDAS model we obtain a simulated (aggregated) value over the quarter for model 3:

To obtain simulated values for model 3 over months t + 1, t + 2 and t + 3, we divide: by h = 3 i.e. .

To preserve dependence but also the inter-temporal dynamics, the residuals for the AR(1) and VAR(1) models are:

Even though the residual vectors for the AR(1) and VAR(1) models should be independent and identically distributed (i.i.d), this is assessed globally and may not be the case for a subset of residuals. For example, if our residual draw for the MIDAS model was from a quarter that saw a significant decrease each month, we also want the residuals over that entire quarter to be drawn for the AR(1) and VAR(1) models. The simulated values for the AR(1) and VAR(1) models are:

where denote the one-step ahead forecasts from models 1 and 2.

We also need the forecast for variable 2 in the VAR(1) model i.e.:

The simulated value at t + 1 is now the average across the three models i.e.:

is now used as the value for in the AR(1) and VAR(1) models. The simulated value for the next period is therefore:

where are the AR(1) and VAR(1) forecasts conditional on from equation 13 and:

This is repeated until horizon h and over horizon h obtained via aggregation:

with the PI calculated using percentiles from the simulated distribution of _{.
If only combining models that forecast iteratively, we modify the above to exclude the MIDAS model. The residual matrix would be:}

and the residuals draw would be one row at a time. The residuals would be added to the forecasts from each equation as before.

The average value of would then be used to generate the forecast next period for each model. If only combining MIDAS models, the residuals would also be a random draw from a single row. If only combining MIDAS models, the residuals would also be a random draw from a single row.